semantics

The red clover, a discolored suit, the autumn leaf, amanita muscaria (aka. fly agaric), the trefoil, the rosy cross, the cup of wine, the bloody club, the tree of life, the Vitruvian Man, Crimson & Clover, etc.

construction

Place an equilateral triangle, a rectangle, and five circles in a simple configuration such that an outline resembling a clover is formed.

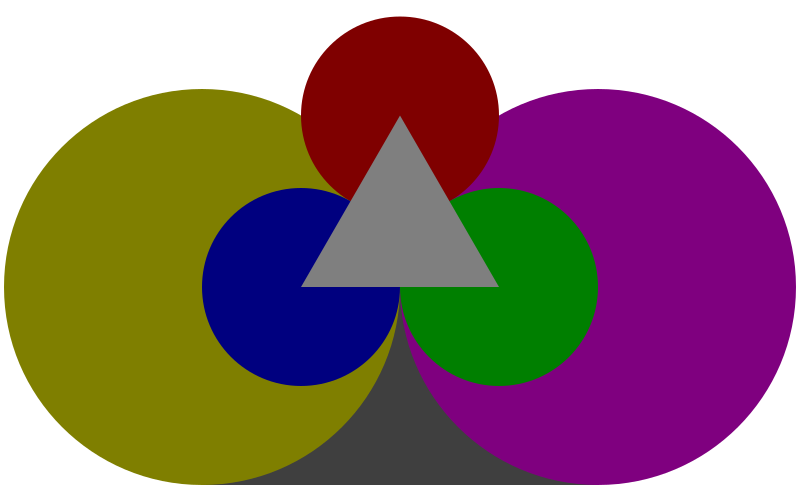
• Let r be the radius of the three identical smaller circles.
• Then 2r is the base of the triangle, as well as the radius of the two identical larger circles.
• The height of the triangle is (* r (sqrt 3)).
• The rectangle in the back simply rests at the bottom, with dimensions of, say, 4r by 2r.

Notice that for the three smaller circles to kiss each other, the topmost circle does not rest strictly above the other two, in a latitudinal sense, but instead "sinks down" between them to a certain extent. We calculate the amount of that "sinking" by subtracting r from the height of the triangle, then subtracting the resulting difference from r again.

• Let us call this amount q = (- r (- (* r (sqrt 3)) r)) = (* r (- 2 (sqrt 3))).

For greater aesthetic appeal, we use this q to tweak the composition into a more "clover-like" shape.

A space is inserted between the bottom two smaller circles. The space equals (* q (sqrt 3)). The multiplication of (sqrt 3) here is quite arbitrary, but an attractive coincidence results from it (as we will soon see, the height of the stretched triangle gets very close to the radius of the stretched larger circle).

To cover the newly inserted space, the base of the triangle is extended by the same amount of (* q (sqrt 3)), and the height of the triangle is increased to preserve equilaterality.

The radius of the larger circles is stretched by (/ (* q (sqrt 3)) 3) (= the newly inserted space divided by 3), while keeping the circles' respective centers fixed at the edges of the two smaller circles.

The topmost smaller circle is shifted rightward by (/ (* q (sqrt 3)) 2), assuming that the space between the bottom two smaller circles was introduced by moving the right-side circle rightward.

For better symmetry, the triangle is also shifted down by (/ (* q (sqrt 3)) 3).

We get the width of our clover by measuring from the edge of one of the bottom smaller circles to the other. To make the height of our clover equal to its width, the rectangle at the back is raised upward. Through a little calculation, we learn that the amount we raise equals (- (- (* r 5) q) (+ (* r 4) (* q (sqrt 3)))) = (- r (* q (+ 1 (sqrt 3)))).

Now, using the image editing program, take the graphical difference of the rectangle and the two larger circles to get the "stem" of the clover. Then take the graphical union of everything remaining to get the clover shape.

Finally, color it in with a nice shade of red. This site uses the so-called psychological primary red.